Равнобедренный треугольник имеет две равные стороны и два равных угла. Рассмотрим методы вычисления суммы его внутренних углов и определения величины отдельных углов.
Содержание
Основные свойства углов равнобедренного треугольника
| Элемент | Свойство |
| Углы при основании | Равны между собой |
| Угол при вершине | Отличается от углов при основании |
| Сумма всех углов | Всегда 180° |
Формула суммы углов
Для любого треугольника, включая равнобедренный: Сумма углов = ∠A + ∠B + ∠C = 180°
Пошаговый расчет углов
Если известны все стороны
- Определите равные стороны AB и AC
- Используйте теорему косинусов для угла при вершине A
- Вычислите углы при основании B и C через теорему синусов
- Проверьте: ∠B + ∠C + ∠A = 180°
Если известны два угла
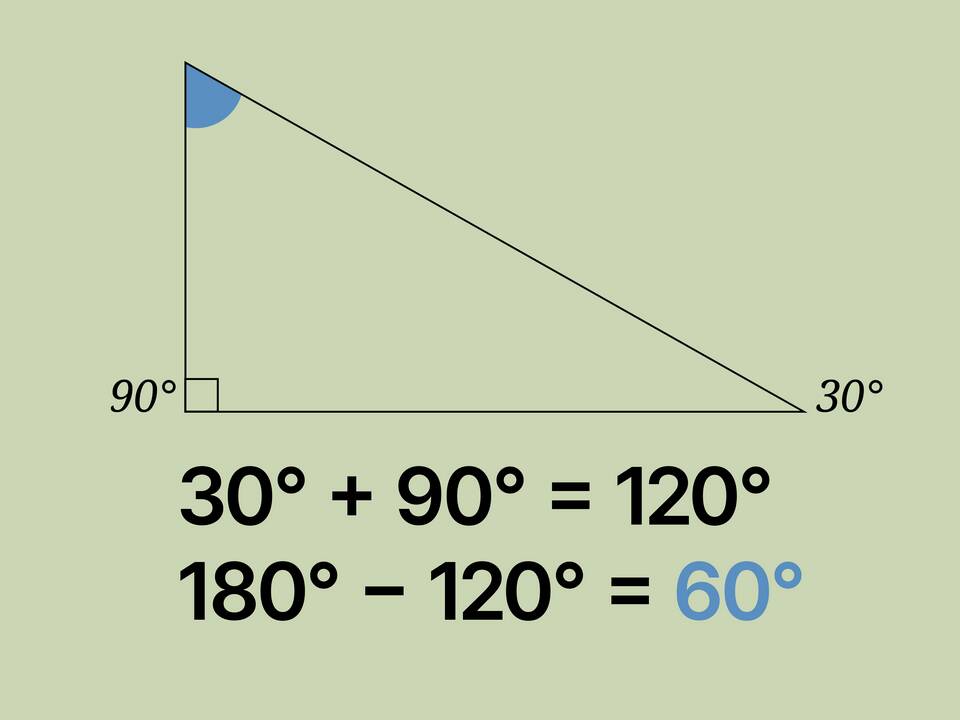
- Найдите третий угол по формуле: 180° - (∠1 + ∠2)
- Равные углы всегда находятся при основании
- Угол между равными сторонами - вершина треугольника
Примеры расчетов
| Дано | Решение |
| Углы при основании по 50° | Вершинный угол = 180° - (50° + 50°) = 80° |
| Вершинный угол 100° | Углы при основании = (180° - 100°)/2 = 40° |
| Один угол 45°, второй 45° | Третий угол = 90° (прямоугольный равнобедренный) |
Особые случаи
Прямоугольный равнобедренный треугольник
Углы: 90°, 45°, 45°
Сумма: 90° + 45° + 45° = 180°
Равносторонний треугольник
Частный случай равнобедренного:
Все углы по 60°, сумма 180°
Практическое применение
- В строительных расчетах
- При проектировании конструкций
- В задачах навигации
- При решении геометрических задач
Проверка правильности вычислений
- Сумма всегда должна быть 180°
- Два угла должны быть равны
- Если все углы равны - треугольник равносторонний
- Не может быть двух тупых углов
Знание свойств углов равнобедренного треугольника позволяет решать широкий круг геометрических задач и применять эти знания в практических ситуациях.